Graph Model
| PartiQL GPML is considered experimental — see RFC-0033. |
Motivation
Graph databases such as Amazon Neptune are becoming more popular for use in applications where the traditional SQL databases and NoSQL databases are inadequate to model data with sprawling relationships. Typically, these kinds of applications are doing path traversals over a graph in a way that would be awkward to express in an equivalently modeled relational database. The question is: can we and should we have a representation in the PartiQL type system that abstracts a graph, provide graph-specific query operations, and unify this with the rest of the type system as we do with relations and structs? Much like the goal of PartiQL is to unify nested data with relational, we should be thinking of graph data similarly.
This proposal introduces the graph data type as a first-class type in the PartiQL type system. The proposal can be seen as a slight generalization of the graph data model in SQL/PGQ specification (ISO 9075-16), which is currently in progress, but has published elements of their work[1]. It is important that PartiQL aligns to an SQL standard that arises around graph query insofar as it is practically acceptable.
Subsequent RFCs are expected for the particular syntax around graph query itself (beyond straw proposals to demonstrate the model and how it would operate in PartiQL) and for the syntax for expressing or serializing/de-serializing graph data directly (similar to struct or bag expressions) to/from PartiQL.
Graph Data Type
To introduce the PartiQL graph data type, we can first consider the other aggregate data types (i.e., those containing PartiQL values) such as bag, list, and struct. We can use the struct and list data types as helpful examples. The struct data type is a collection of members that have an attribute name associated with any PartiQL value.
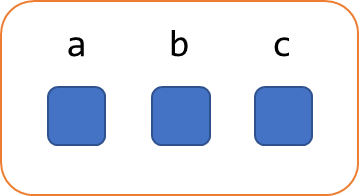
In the above, PartiQL models the attribute names and the association to the attribute’s values as a property of the struct, not a property of the value contained within the struct. This is important, and is also indicative of how we extract these associations in PartiQL:
SELECT a, v FROM UNPIVOT my_struct AS v AT aIn this case we use the UNPIVOT operator to bind to a variable the attribute names associated to the struct’s members.
This query can be read informally as “find all a and v such that a : v is an attribute/value
pair in my_struct.”
The list data type similarly models the association of position ordinal to member value.
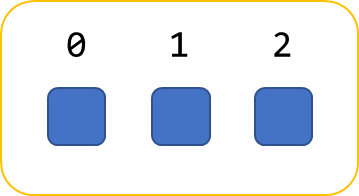
Which is similarly extracted as variables:
SELECT i, v FROM my_list AS v AT iFor the graph data type, we model something very similar. A graph is a collection of vertices and edges, where edges connect pairs of vertices and can be directed or undirected. Vertices and edges have labels (similar to the attribute names in struct). There is also a value at each vertex and edge, which can be any PartiQL value.
The following example illustrates the model:
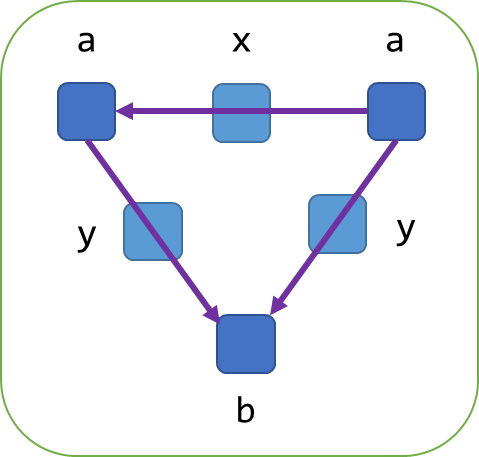
In the above, we have a graph with three vertices, two labeled a and one labeled b. We have three edges, one
labeled x and two labeled y. The relationships of the edges to their respective vertices are fully contained
within the graph. All values within the graph, either at an edge or at a vertex, can be any PartiQL value. This generalization
is consistent with the other container types and fits nicely in PartiQL’s data model. This also means that PartiQL
graphs could have vertices or edges that themselves be graphs, and likewise values can be as simple as scalar values.
As an important example, labeled property graphs (LPG) of the GPML paper[1] are modeled straightforwardly in PartiQL: a value at each vertex and edge is restricted to be a PartiQL struct.
Similarly, Resource Description Framework (RDF)[2] graphs could be modeled in PartiQL by having non-literal, non-blank
vertices and edges labeled by URI strings with their values being NULL. RDF literals could be a NULL labeled node with
their value being any corresponding PartiQL value (this is a generalization of RDF as literals are only strings in RDF’s
model). RDF blank nodes can be denoted with a label that never conflicts with URI such as :my_blank ( is
never a valid scheme for a URI).
Even though PartiQL defines a very general graph data model, it is not required that a host database actually supports arbitrary values at vertices or edges. This is similar to PartiQL over a relational database, where attributes of a row are restricted to scalars.
Addition to the PartiQL Data Model
As outlined above, graphs are introduced as a new category of "native" values in the PartiQL data model, on par with scalar literals, structs, lists, and bags:
<partiql value> ::=
<absent value>
| <scalar value>
| <tuple value>
| <collection value>
| <graph value> //newConsequently, graph values can occur as members of structs, bags, and lists.
Graph Data Model
For graph values themselves, rather than giving a grammar—as the PartiQL specification does for other values—we will define an abstract data model, largely following the one for GPML[1]. We do this because a concrete syntax for graph literals could emerge from ISO/IEC standardization, possibly as part of GQL, but no public information is yet available about that effort. When appropriate, graph literals in PartiQL would be covered in a separate RFC.
A graph (a PartiQL graph value) is a tuple
< Nodes, Edges, ends, labels, payload >
where
-
Nodes is a finite set of the nodes of the graph;
-
Edges is a finite set of the edges of the graph;
-
ends : Edges → (Nodes x Nodes) union { {u,v} | u, v in Nodes }
is a total function mapping each edge to its endpoints, which are an either ordered or an unordered pair of nodes; -
labels : (Nodes union Edges) → P( string_value ) is a total function that maps each node and each edge to a set of string labels;
-
payload : (Nodes union Edges) → partiql_value \ {
MISSING} is a total function that maps each node and each edge to its payload, which is a PartiQL value that cannot beMISSING.
The inhabitants of the sets Nodes and Edges are understood abstractly; all that is known about them is given by the functions ends, labels, and payload. Intuitively, one can think of graph nodes and edges as uninterpreted identifiers, perhaps corresponding to some implementation-specific memory locations.
The primary difference of this graph definition from the property graph in GPML[1] is
the payload function. In a GPML property graph, its analogue is the partial function
π : (Nodes union Edges) x PropertyNames ⇀ Values
that,
for each node (or an edge), associates some of the available property names to values.
This effect can be obtained with payload by using PartiQL structs as its values,
with property names keys within them.
Consequently, most comments and examples for property graphs given in [1] apply to the
definition here as well.
Returning to the example from the introductory section above, the graph value is described, according to this definition, as follows:
-
Nodes = { n1, n2, n3 }
-
Edges = { e1, e2, e3 }
-
ends(e1) = (n2, n1), ends(e2) = (n1, n3), ends(e3) = (n2, n3)
-
labels(n1) = {"a"}, labels(n2) = {"a"}, labels(n3) = {"b"}
-
labels(e1) = {"x"}, labels(e2) = {"y"}, labels(e3) = {"y"}
(With the payload function elided, as values at nodes and edges were not specifically considered in the example.)
Drawbacks
This will be a sizable extension of the data model and the language.
It will require substantial specification and implementation effort
(smaller, but on the order of magnitude of what is already in PartiQL).
It is possible that some implementations of PartiQL might not be willing
to take on this effort. This might make more acute the need for
some sort of a mechanism for PartiQL subsets or profiles
and for dealing with subsequent complexities in both specification and
reference/toolkit implementation of the language.
Rationale and Alternatives
Some earlier discussions of graph support for PartiQL indicated that a reference type (i.e., pointer or alias) could “solve” adding graph data for PartiQL. While this primitive could be used to construct graphs, it would not have the same degree of abstraction as the proposed data type and it creates and issue that an associated value that is not fully contained within a PartiQL value.
The abstraction problem can be illustrated by the LPG example, how might we solve this with references? Since scalars themselves are atomic values, references would have to be contained in some container type such as a list or struct. Now vertices must be a struct or a list, and now we’re defining a convention which is a substitution for strong typing. Another problem in the abstraction is how do we model properties on the edges and multiple edges for a given label? Again, we need to now model the edge property from the source as either a list/bag of references or a single reference and we need to introduce an intermediate struct between the two vertex struct values with some convention. Assuming we defined this convention, how would a different graph model work such as RDF? Another convention could be defined but now we have the problem of how do we determine if the convention is being used or not (e.g., valid for a MATCH sub-clause)--this is introducing the concept without typing the concept. If the answer is schema—that is the same as saying we have some kind of notion of static type. References are being used here to serve as a potential implementation detail that leaks into the logical model. A similar rationale could be used for the list data type. The relational model could easily represent a list as a bag of structs containing an ordinal and value—but PartiQL has a first-class type because it is often the case that we have operations directly on lists that are of value (e.g., accessing an element by ordinal).
Occurrences of MISSING Within a Graph
In the definitions as given so far, MISSING is not allowed to occur within a graph
(unless embedded within another PartiQL value occurring within a graph).
That is, MISSING cannot be a label (or used instead of a label set at a node or edge)
and MISSING cannot be a value at a node or edge. Philosophically, this choice comes
from an intuition that a graph value is more akin to a struct value (which does not allow
MISSING at an attribute) than to a collection (which allows MISSING as a member).
However, there could be reasons to make different choices.
Graph Construction
While outside the scope of this document to define such syntax, it is important to consider how graph data types might be serialized or constructed. A database could implement a view over a relational representation of a graph with this data type. This pattern is seen in databases such as Oracle, where a set of tables can be treated as a graph. Likewise, PartiQL could adopt minimal syntax extensions from something like Cypher[3] to unify its DML with graph manipulation. Also, similar to bag, list, and struct constructor expressions, we could introduce graph constructor expressions to create graph values (e.g., literals in expressions).
Graph Query
While query syntax and semantics is also outside the scope of this RFC, let us consider a straw example of what a PartiQL graph query could look like and mean with respect to this data model.
SELECT the_a.name AS src, the_b.name AS dest
FROM my_graph MATCH (the_a:a) -[the_y:y]-> (the_b:b)
WHERE the_y.score > 10In the above example, the MATCH sub-clause is working similar to how UNPIVOT works, it is effectively saying find
all the_a, the_y, and the_b such that the graph pattern matching association holds. These names are
then bound to variables that are then usable in other clauses. In other words, the loose specification of the MATCH
sub-clause is that it returns a bag of variable bindings much like any other FROM source. Similar to the way list
ordinals and struct ordinals work, the relationship matching in the graph operators are scoped to a single graph
instance and has no implications outside of that value. Such a MATCH clause could be as complex as needed (having
other sub-clauses) to perform the appropriate graph query constructs.